Teorema de Thévenin


Enunciado

El Teorema de Thévenin establece que “si una parte de un circuito eléctrico lineal está comprendida entre dos terminales A y B, esta parte en cuestión puede sustituirse por un circuito equivalente que esté constituido únicamente por un generador de tensión en serie con una resistencia de forma que al conectar un elemento entre las dos terminales A y B, la tensión que cae en él y la intensidad que lo atraviesa son las mismas tanto en el circuito real como en el equivalente".
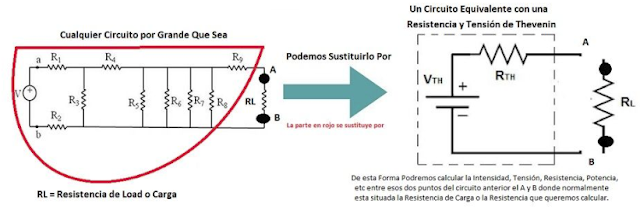Circuito eléctrico completo (izquierda), Circuito eléctrico equivalente de Thévenin (derecha)















Por equivalente se entiende que su comportamiento ante cualquier red externa conectada a dicho par de nodos es el mismo al de la red original.

Características

  • Usa fuente de tensión en su circuito.
  • El modelado de su circuito con respecto a la fuente y resistencia o impedancia, es conectada en serie.
  • El voltaje thévenin se define como la tensión que aparece entre los terminales de la carga cuando se desconecta la resistencia de la carga.
  • La resistencia thévenin existe entre los puntos A y B sin la resistencia de carga y poniendo en cortocircuito a todas las fuentes, es decir, reemplazándolas por un conductor.

Aplicaciones

Básicamente el teorema de thévenin consiste en facilitar el análisis de los circuitos eléctricos debido a su efectiva simplificación, entre sus usos cotidianos están:

  • Reducción de circuitos y redes complejas en una forma que permita facilitar su análisis, es decir, puede determinar la resistencia o impedancia equivalente de un circuito grande en simplificar bastante sus cálculos. Por ejemplo, el circuito eléctrico de un carro, una edificación y hasta en los aparatos electrónicos de uso cotidiano.
  • Prevención y localización de fallas en circuitos.
  • Análisis de estabilidad en redes de potencia eléctrica.
  • Determinar parámetros de semiconductores y dispositivos piezoeléctricos (sirven para medir presión, aceleración y tensión a través de la lectura de señales eléctricas).



Pasos para su aplicación

1) Retirar la resistencia RL del circuito, o sea abrir el circuito por ese lado.

2) Para encontrar la resistencia thévenin se cortocircuita las fuentes de voltaje y se abren las fuentes de corrientes.

3) Para hallar la tensión thévenin tiene que estar desconectado la resistencia RL.

4) Unir la resistencia al circuito equivalente.

Ejercicios

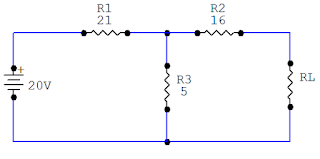
Calcular la resistencia thévenin y tensión de los siguientes circuitos:

Circuito 1


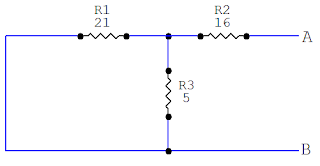
Abrimos la carga RL, entonces la resistencia R2 queda en el aire debido a que por allí no pasa corriente, por lo tanto la descartamos. Ahora a encontrar el voltaje thévenin.

Para hallar el voltaje thévenin vemos en el circuito que la corriente pasa entre estos dos puntos rojos señalados.

Entonces tenemos que hallar la corriente (I).


Ahora teniendo la corriente, hallamos el voltaje thévenin.


Procedemos a cortocircuitar la fuente de alimentación para hallar la resistencia thévenin.


Viendo el circuito se ven dos resistencias en paralelos (R1 y R3), hacemos su respectivo calculo y lo sumamos con la resistencia en serie (R2).
Obteniendo la resistencia thévenin.

Por lo tanto el circuito resuelto con el teorema de Thévenin queda como:

Circuito 2

Abrimos la carga RL.

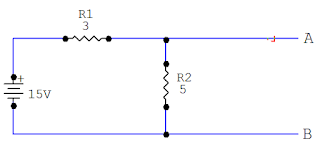
Para hallar la resistencia thévenin del circuito, tendremos que poner la fuente en corto.
Notese que las resistencias R1 y R2 están en paralelos al igual que las resistencias R3 y R4, por lo tanto se procede a calcular para obtener la resistencia thévenin del circuito.
Ahora pasamos a medir la tensión de thévenin del circuito, por si se dan cuenta al momento que se quitó la carga RL del circuito, las resistencias R3 y R4 quedaron al aire, es decir, no pasa corriente en ellos, por lo tanto los descartamos y ahora calculamos el voltaje entre estos dos puntos rojos señalados.
Aplicamos la formula de divisor de voltaje entre los puntos A y B, para así hallar la tensión de thévenin.
Ya terminando, el circuito equivalente thévenin para este circuito queda como:

Referencias

Suscribirse a: Entradas (Atom)