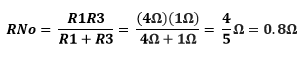Teorema de Norton

Edward Lawry Norton

Enunciado

El teorema de Norton dice "Un generador de tensión en serie con una resistencia o impedancia, puede ser sustituido por un generador de corriente en paralelo con la misma impedancia o resistencia, y viceversa".
Circuito eléctrico (izquierda), Circuito equivalente de Norton (derecha)

Por equivalente se entiende que su comportamiento ante cualquier red externa conectada a dicho par de nodos es el mismo al de la red original.

Características

  • Usa fuente de corriente en su circuito.
  • La resistencia Norton tiene el mismo valor que la resistencia de thévenin, es decir, se consigue del mismo modo.
  • El circuito Norton equivalente consiste en una fuente de corriente Ino en paralelo con una resistencia Rno.
  • La corriente de Norton se calcula como la corriente que circula por el equivalente de Thévenin poniendo en cortocircuito a los terminales A y B.

Aplicaciones

El teorema de Norton es dual al de thévenin, es decir, para el análisis de los circuitos eléctricos los dos teoremas se relacionan o coordinan entre sí en su posterior resolución. Entre algunas aplicaciones de este teorema están:
  • Calculo de nodos y puntos circuitales.
  • La prueba de componentes de redes y circuitos interconectados.
  • Conocer las condiciones en las que se da la máxima transferencia de potencia de un sistema.
  • Esta técnica es aplicable en redes eléctricas.
Pasos para su aplicación

Con respecto a los pasos para aplicar el teorema de norton son dos formas de resolver este teorema. A través del uso del teorema de thévenin y al hallar RTh y VTh, podemos usar esos dos valores para obtener las variables del teorema de norton porque:
  • La resistencia thévenin (RTh) es igual a la resistencia norton (RNo).
  • La corriente de norton (INo) la podemos obtener mediante el uso del voltaje thévenin (VTh) y la resistencia thévenin ( RTh), usando la ecuación que se ve a continuación.
Es por eso que el teorema de norton es dual al teorema de thévenin, ya que se relacionan entre si y son equivalentes.

La otra forma ahora sería ya por definición del enunciado del  teorema de norton, entre los pasos a llegar están:

 1) Analizar el circuito.

2) Verificar las fuentes de corriente y de tensión.

3) Calcular la corriente norton (INo).

4) Abrir las fuentes de corriente.

5) Calcular la resistencia norton (RNo)


6) Obtener el circuito equivalente norton, colocando la fuente de corriente y la resistencia norton en paralelo.

Ejercicios

Circuito I: 

 Vamos a calcular primero la resistencia de norton (RNo), procedemos a quitar la carga RL
Como se podrá ver las resistencias R1 y R3 están en paralelo

Calculamos ahora la corriente norton (INo), como se ve en el diagrama, hay presencia de dos fuentes, el cual la corriente (I1), de la malla 1 será diferente a la corriente (I2) de la malla 2. Por lo tanto la corriente norton (INo) se calculará como:

Entonces la corriente norton queda como


Para terminar, se dibuja el circuito equivalente del teorema de norton poniendo la fuente de corriente en paralelo con la resistencia norton.

Circuito II

Esta vez resolveremos el circuito a través de la relación entre el teorema de norton y el teorema de thévenin.


Procedemos a hallar la resistencia thévenin (RTh), lo cual cortocircuitamos la fuente y el circuito quedará así. Entonces ahí se ve que las resistencias R1 y R3 están en paralelo, procedemos a su calculo y al unirlo con la resistencia R2 conseguiremos la resistencia thévenin (Rth).


Ahora vamos a hallar la tensión thévenin (VTh), en el circuito se ve que la resistencia R2 está al aire debido a que por ella no pasa corriente por allí, por lo tanto vamos a calcular la tensión entre los dos puntos rojos señalados.

Ahora ya teniendo la tensión thévenin ( VTh) y la resistencia thévenin (RTh), podemos hallar las dos variables del teorema de norton.

  • Resistencia norton (RNo) = La Resistencia thévenin.
  • La corriente norton (INo) se consigue a través de las variables de thévenin.

Ya teniendo la corriente norton (INo) y la resistencia norton (RNo), dibujamos el circuito equivalente del teorema de norton.

Referencias

Suscribirse a: Entradas (Atom)